Abstract
Methods are developed to acquire and track orthogonal frequency division multiplexing (OFDM) digital FM radio signals. These methods are being developed with the goal of using FM signals’ pseudorange and accumulated delta-range observables to navigate. Delay lock loop and phase lock loop discriminator outputs are computed by solving an optimal fitting problem in the frequency domain for each OFDM symbol. Single-differencing of the signals’ observables between a roving user receiver and a reference station receiver can remove transmitter clock drift effects. Wideband data collected in Roanoke, Virginia, and in Charlotte, North Carolina, have been processed offline and used to study these signals’ suitability for navigation. Single-differenced pseudorange measurement and bias errors relative to a base station can be on the order of 100 m, but single-differenced accumulated delta-range precision can be better than 0.1 m. A system that uses accumulated delta range may be able to yield 5-m level positioning accuracy if multipath effects can be compensated for. The present study represents an initial effort toward the goal of achieving this level of accuracy. Only pseudorange-based navigation is tested here, however, and its observed errors are on the order of 500 m.
1 INTRODUCTION
The known vulnerabilities of GNSS in general and GPS, in particular, have spurred a search for alternative navigation methods. One class of methods relies on radio frequency (RF) signals of opportunity such as Digital TV or LTE signals (Kassas et al., 2014; Raquet et al., 2007; Schexnayder et al., 2008; Shamaei & Kassas, 2018; Yang et al., 2012; Yang & Nguyen, 2013, 2015; Yang & Soloviev, 2018). Another signal of opportunity is FM radio. It has been considered in Fang et al. (2009), Giordano et al. (1994), Krumm et al. (2003), and Popleteev (2011). The navigation method of Giordano et al. (1994) uses the phase of the FM signal’s 19-KHz pilot tone. The methods of Fang et al. (2009) and Krumm et al. (2003) use FM signal power as the observable. The method of Popleteev (2011) uses FM signal fingerprinting.
The present paper is part of an effort to use digital FM orthogonal frequency division multiplexing (OFDM) signals as radionavigation signals of opportunity. Important properties of these signals are described in iBiquity Digital Corporation (2001, 2007). This effort seeks to derive traditional pseudorange and beat carrier-phase observables from OFDM signals, much like their GNSS counterparts, and use them to navigate. To the best of the authors’ knowledge, this is the first effort to use the OFDM digital part of FM signals for navigation purposes.
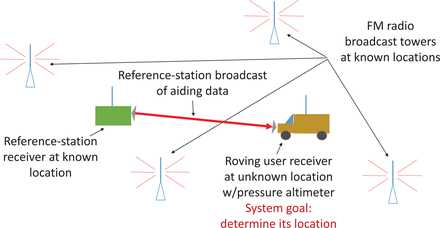
Figure 1 depicts a candidate navigation system that is based solely on digital FM signals’ observables and altimeter data. If three or more FM towers are visible to the roving user receiver and if they have sufficient geometric diversity, then pseudoranges from these signals can be combined with the rover’s altimeter to deduce three-dimensional (3D) position and time. The transmitter clocks are low quality. Their frequency standards can have errors as high as 10−6 sec/sec. Therefore, a reference station at a known location is required in order to observe and compensate for the transmitter clock errors.
FM signals-of-opportunity navigation concept
There are several advantages to using FM signals as navigation signals of opportunity. First, they have wider coverage than LTE or WiFi signals. Therefore, a system based on FM signals would only require the transmitter locations and transmitter clock corrections of a relatively small number of stations. The transmitter locations tend to be well surveyed and change infrequently, making the location almanac easy to initialize and maintain. Second, the long wavelength of FM signals, on the order of 3 m, makes them able to penetrate many buildings. Therefore, they are available in many indoor environments. Third, they have high signal powers, which allows signals to be acquired and tracked easily. Fourth, the OFDM part of the signal includes absolute timing information, except that there is a 1.4861 sec frame count ambiguity. This timing information can enable correlation between reference station and rover reception times without the need for a high-bandwidth data link. Fifth, the OFDM modulation enables a receiver to deduce traditional beat carrier phase in a straightforward manner. This fact allows a navigation system to use the corresponding precise accumulated delta-range observable.
There are drawbacks to using FM signals. The FM OFDM signal consists of two bands that are each 69.4-KHz wide, one centered 163.9-KHz below the carrier and the other centered 163.9-KHz above the carrier. The net bandwidth is much narrower than even the GPS C/A code. This narrowness allows potential multipath errors to be much larger than for GPS C/A code. Furthermore, although FM broad-cast antennas may employ circular polarization, user equipment antennas tend not to use circular polarization. Therefore, the user equipment does not exploit circular polarization effects in order to reduce multipath interference. Another disadvantage of FM signals is that they tend to have less geometric diversity than LTE or WiFi signals.
The goals of the present paper are to develop, implement, and test algorithms to acquire and track digital FM OFDM signals and derive the navigation observables pseudorange, beat carrier phase, and carrier Doppler shift. Achievement of these goals will yield a receiver system that enables the use of digital FM OFDM signals as navigation signals of opportunity. The strategies that are employed to achieve these goals are to: a) implement an acquisition search for OFDM symbol timing and carrier Doppler shift; b) devise discriminators for symbol timing and beat carrier phase; c) implement signal tracking using a delay lock loop (DLL) for symbol timing and a phase lock loop (PLL) for beat carrier phase; and d) deduce pseudorange from symbol timing and accumulated delta range from beat carrier phase.
This paper makes seven contributions on the subject of digital FM navigation using OFDM signals. First, it defines and implements an appropriate all-channels RF front-end architecture and a per-channel digital pre-processing architecture that are suitable for using digital OFDM signals for navigation purposes. Second, it develops a new decision-directed combined DLL/PLL discriminator based on decoding QPSK symbols and then solving a frequency-domain data fitting problem. Third, it develops a carrier-aided symbol timing DLL that uses a second-order proportional/integral feedback scheme in order to compensate for the large code/carrier divergences that can occur on digital FM signals. These first three contributions have many similarities to techniques that others have developed to process OFDM signals (e.g., see Shamaei and Kassas [2018]). This paper’s contribution consists of being the first to combine them in an architecture that is suitable for deriving navigation observables specifically from digital FM OFDM signals.
This paper’s fourth contribution is to develop algorithms for computing pseudo-range and accumulated delta range from DLL and PLL outputs. It also develops a means of performing receiver-to-receiver single-differencing of pseudorange and accumulated delta range in a manner that removes the effects of transmitter clock offset and drift. Fifth, it uses real data to explore the properties of actual digital FM OFDM signals under static and dynamic conditions. This study documents the possible high precision of accumulated delta range, the low precision of pseudorange, and the significant multipath effects that can occur. Sixth, this paper develops a new method to reduce multipath effects in accumulated delta range through the exploitation of carrier Doppler shift diversity. Seventh, it computes and evaluates navigation solutions that use only single-differenced pseudoranges from digital FM OFDM signals along with pressure altimeter data.
This paper represents the initial study in a planned series of studies on the feasibility of navigation based solely on digital FM OFDM signals. The eventual goal is to achieve two-dimensional (2D) accuracy on the order of 5 m based on carrier-phase techniques applied to a user receiver that moves relative to fixed transmission towers. That user could be a ground vehicle, or it could be an airplane that was also equipped with a pressure altimeter. Such a system could provide a backup to GNSS. This study offers some hope of that eventual level of performance, but there are still significant challenges to be met in order to realize that hope.
This paper presents its developments in seven main sections followed by a summary and conclusion. The second section reviews the characteristics of digital OFDM signals. It also defines an RF front-end and subsequent signal processing that can be used to mix a particular channel’s OFDM signal to baseband. The third section reviews an OFDM signal acquisition algorithm and presents results that apply it to real data. The fourth section develops DLL and PLL discriminators and their corresponding tracking loops, and it gives results for their application to real data. The fifth section presents formulas for computing raw pseudorange and accumulated delta range along with receiver-to-receiver single-differenced pseudorange and accumulated delta range. This section also presents static-receiver results that give an indication of the navigation precision that could be available from single-differenced pseudorange and accumulated delta range. The sixth section documents extreme multipath effects that have been observed during dynamic tests which involve a roving user receiver that is driven along a freeway at high speed. This section also outlines a method for ameliorating the effects of multipath on accumulated delta range. The seventh section uses pseudorange measurements from a dynamic test to perform the first evaluation of the potential of digital FM OFDM signals to provide a navigation capability. The eighth section proposes areas for possible further study. The ninth section summarizes this paper’s findings and presents its conclusions.
2 DIGITAL FM OFDM SIGNAL MODEL AND INITIAL PROCESSING
2.1 Signal Model and Characteristics
The digital FM OFDM signal uses standard OFDM inverse fast Fourier transform (FFT) techniques in order to define its modulation. Its important features that are relevant for navigation purposes are documented in iBiquity Digital Corporation (2001, 2007). The broadcast signal can be modeled as follows:
1
where A is the carrier amplitude; fc is the nominal carrier frequency in Hz; ϕ0c is the initial carrier phase in radians; i is the OFDM symbol count index; Ts = 2160/ Fs = 0.002902494331066 sec is the nominal symbol period; k is the frequency index; nik is an encoded QPSK symbol that takes on an integer value of zero, one, two, or three, or a BPSK symbol that takes on an integer value of zero or two; and Fs = 744187.5 Hz is the fundamental FFT/inverse-FFT sampling frequency of the OFDM encoding.
The function h(t) in Equation (1) is a raised-cosine windowing function that is one symbol in length. It has 112 sample initial and final raised-cosine attenuation sections. Its formula is:
2
where Δts = 1/ Fs = 1.343747375493407 × 10−6 sec is the fundamental FFT/ inverse-FFT sample interval. The function h(t) is positive over the entire symbol interval Ts, and Ts is longer than the FFT period 2048Δts. Therefore, the digital FM OFDM signal has a cyclical prefix whose duration equals the excess time of the symbol interval: Ts – 2048Δts = 112Δts.
The two k summations in Equation (1) can be interpreted as being part of an inverse Fourier series. Suppose that one defines complex Fourier coefficients as follows:
3
Then, the last two summations in Equation (1) can be re-written in the following inverse Fourier series form:
4
This property will be exploited in later signal processing calculations, as is typical in OFDM signal processing.
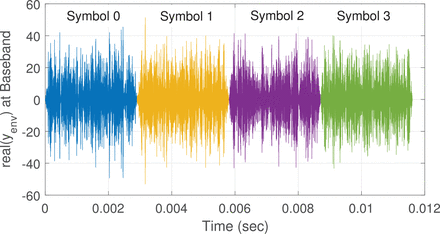
The time-domain properties of the signal’s complex envelope are illustrated in Figure 2. It plots the real part of the complex envelope function for four simulated symbols. The envelope’s real part equals the real part of the formula in Equation (1) after removal of the carrier term 
. The imaginary part of the envelope, although not shown, looks similar. The fades at the beginning and end of each symbol are caused by the raised-cosine envelope function h(t). The seemingly random oscillations during the center portion of each symbol are the results of the QPSK symbol phasings in nik for k = −546,…,−356,356,…,546.
Example digital FM OFDM real-part envelope of a four-symbol time history
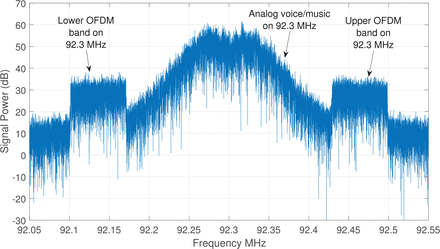
An experimentally recorded spectrum of a typical digital FM OFDM signal is shown in Figure 3. The large trapezoidal peak centered at the 92.3-MHz carrier is the FM-modulated analog channel. The OFDM signal is contained in the two flat side bands, the lower one extending from 92.101 MHz to 92.171 MHz and the upper one extending from 92.429 MHz to 92.499 MHz in the figure. The lower band corresponds to the k summation from −546 to −356 in Equation (1), and the upper band corresponds to the k summation from 356 to 546. The digital FM OFDM band is extensible to include additional values of k in the range −355 to 355. The present work does not consider the use of these optional bands.
Example digital FM OFDM spectrum in 92.3-MHz band
The total number of frequency bands and transmitted symbols per symbol interval equals the total number of k indices in the two summations; 382. 22 of these bands are designated as reference bands. They occur every 19th band. The reference bands correspond to the 22 k index values {−546, −527, −508, …, −356, 356, 375, 394, …, 546}. Each of these bands is restricted to transmit BPSK symbols so that their nik symbols can take on the values zero and two only. All of the other 360 frequency bands that correspond to the other 360 k values transmit QPSK data symbols. Thus, their nik symbols can take on any integer value in the range from zero to three.
The 22 reference frequencies transmit housekeeping information. Every 32-symbol period is designated as a frame. Each reference frequency starts its frame with a 7-bit synchronization pattern that is differentially encoded. The pattern is 0110010, with the earliest received bit being the most significant bit and the latest received bit being the least significant bit. The 17th through 20th bits of each frame are used to differentially encode a frame counter that repeatedly counts from zero to 15. This count allows for the determination of absolute time according to the symbol transmission clock to within an ambiguity of 16 × 32 × Ts = 1.486077097505669 sec.
2.2 RF Front-End Operations and Initial Per-Station Digital Signal Processing
The navigation concept of Figure 1 requires the system to be able to receive FM signals from multiple stations and process them in a way that will yield identical or nearly identical time delays through the system. This presents a challenge because each different station broadcasts on a different nominal carrier frequency fc. In the U.S., there are 100 possible nominal carrier frequencies, fc = 88.1 MHz,88.3 MHz,88.5 MHz,…, 107.9 MHz.
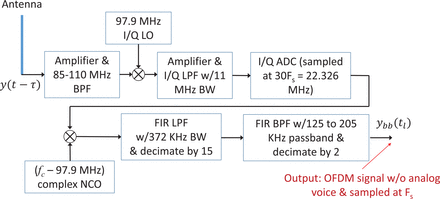
A suitable approach to capture all possible signals in a time-coherent manner is to have the RF front-end do the following: a) mix the entire 20-MHz FM band to complex baseband; b) low-pass filter the result to attenuate frequencies more than 10-MHz away from baseband; and c) sample and digitize the resulting signal at a frequency of at least 20 MHz. Such a system has been implemented using a universal software radio peripheral (USRP). The particular design that has been implemented for purposes of this study is shown in the top half of Figure 4. The baseband mixing frequency is 97.9 MHz. The final sampling frequency is 30 Fs = 22325625 Hz.
Block diagram of RF front-end processing for all bands and subsequent digital signal processing for the single band with nominal carrier frequency fc
The lower-half of Figure 4 defines the digital signal processing that is needed to mix a particular FM station’s signal to baseband—the one with a nominal carrier frequency fc—and to perform additional finite impulse response (FIR) filtering and decimation in order to produce the final output signal ybb(tl) at the nominal OFDM FFT/inverse-FFT sampling frequency Fs.
This final chain of signal processing starts by mixing out the nominal intermediate frequency signal fc −97.9 MHz. Next, it performs FIR low-pass filtering to remove the other FM stations from the signal, followed by decimate-by-15 down-sampling. Lastly, it performs FIR band-pass filtering to remove the station’s central analog voice/music signal and any noise below −198.6 KHz and above +198.6 KHz. The resulting output contains only the digital FM OFDM part of the signal whose nominal carrier frequency is fc.
A reasonable model of the complex baseband sampled signal at the output of the RF front-end during the i-th symbol interval is:
5
where tl = t0 + lΔts is the l-th sample time, Ai is the received signal amplitude, fDopp,i is the carrier Doppler shift, ϕi is the (negative) beat carrier phase at time τi, and τi is the time of arrival of the leading edge of the symbol at the output of the signal processing chain shown in Figure 4. This model is valid for all sample times tl that fall within the i-th symbol interval (i.e., for all tl such that τi ≤ tl < τi + Ts).
In theory, there should also be symbol Doppler shift. That is, the time argument (tl – τi) should be multiplied by the factor (1 + fDopp,i/fc) in the three right-most places where it appears in Equation (5). In practice, the factor fDopp,i/fc is very small and can be neglected over a single symbol interval. Its main impact is on the time differences between successive symbol reception times (e.g., on τi+1 –τi) This effect is part of the reason why these differences do not exactly equal the nominal symbol period Ts.
As with GNSS signal models, the received carrier Doppler shift fDopp,i and the received symbol arrival intervals τi+1 – τi, τi+2 – τi+1, etc. are affected by range rate, by transmitter clock offset and drift rate, and by receiver clock offset and drift rate. The receiver makes no attempt to sort out the various components that contribute to these observed effects at the signal processing stages that are described in this paper. This is the same approach that is used for GNSS signal processing.
There are special considerations that must be taken into account when processing these OFDM signals. They are addressed using algorithms that are applied after the signal has been output from the RF front-end. This is possible because the sampling rate at the output of the RF front-end, Fs = 1/ Δts, is the sampling rate of the OFDM signal modulation. If the code Doppler shift is not too large, then it is possible to make all of the required adjustments, both for the OFDM modulation and for the multiplicity of FM carrier frequencies, downstream of the signal processing that is described in the present section. The remaining sections of this paper show how to perform the needed operations.
3 OFDM SIGNAL ACQUISITION
The OFDM signal in the output time history ybb(tl) is, in effect, the only signal present. There is only a negligible amount of the voice/music analog signal from the same station because the band-pass FIR filter in the final block of Figure 4 has suppressed it by more than 70 dB. Similarly, there are no signals from other stations because the low-pass FIR filter in the second-to-last block of the figure has eliminated them. The signal-to-noise ratio of the remaining OFDM signal tends to be high, so that one can easily distinguish it from the noise.
These signal properties allow the use of a simple algorithm for the initial determination of symbol timing. The algorithm exploits the underlying periodicity of the inverse Fourier transform form of each OFDM signal, consistent with Equation (4). The period is Tper = 2048 / Fs = 2048Δts. That is, the inverse Fourier series repeats every 2,048 samples. Each symbol, however, is 2,160 samples in length. Therefore, the first 112 samples constitute a cyclical prefix to the signal, and the last 112 samples have the same inverse Fourier series values. The only differences between them are caused by the mirror-image amplitude effects of the h(tl – τi) windowing function during the first and last 112 samples.
The symbol timing search looks for correlation power between the first 112 samples (i.e., the cyclic prefix) and the last 112 samples of proposed sequences of 2,160-sample symbols. The acquisition statistic is computed as follows:
6
where:
7
In these formulas, m is the candidate sample count offset between the first sample and the start of the first symbol. The quantity Nsyms is the number of symbols over which the correlation power is being averaged.
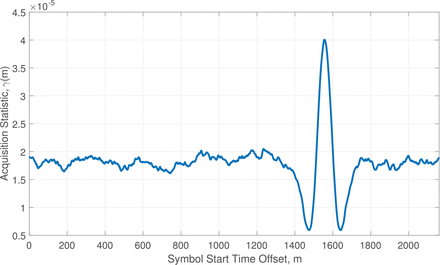
A brute-force search looks for the value of m in the range 0,1,2, …, 2159 that maximizes the acquisition statistic γ(m). An example plot of this acquisition statistic versus m is shown in Figure 5. It plots γ(m) vs. m for a typical acquisition calculation that uses recorded data from the 89.1-MHz NPR station that broadcasts in Roanoke, Virginia.
Example plot of signal timing acquisition statistic versus symbol start time offset
A total of Nsyms = 484 symbols have been used to compute each statistic, which corresponds to an acquisition data interval of (Nsyms + 1)Ts = 1.4077 sec. The obvious peak in this plot at the true symbol offset m = 1554 is typical for strong FM signals. Note that it may be possible to use fewer than Nsyms = 484 symbols and still achieve a reliable acquisition. This timing search is similar to one defined in van de Beek et al. (1998), except that it sums over multiple symbols rather than a single symbol.
The acquisition results can also be used to develop an initial estimate of the carrier Doppler shift. This calculation averages the net carrier-phase rotations over the correlation intervals that correspond to the in-phase and quadrature accumulations of Equation (7). The resulting Doppler shift estimate is:
8
where mopt is the symbol start time offset that maximizes γ(m) (e.g., mopt = 1554 for the acquisition associated with Figure 5). The division by Tper in this formula accounts for the fact that this is the time difference between the first and last 112 samples of a symbol.
This method makes no attempt to compensate for the non-periodic effects of the windowing function h(tl – τi). An improved algorithm might seek to compensate for this effect before computing the Ii(m) and Qi(m) accumulations, the acquisition statistic γ(m), and the carrier Doppler shift ωDopp. This added level of complexity has not been used because the acquisition calculations worked well on real data, despite this lack of compensation and the resultant deviations from the periodicity assumption.
4 DLL AND PLL DISCRIMINATORS, TRACKING LOOPS, AND PERFORMANCE
4.1 Block Diagram and Initial Operations Prior to Symbol Decoding
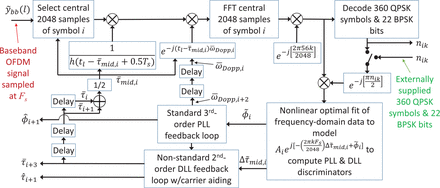
The signal acquisition results are used to initialize a coupled DLL/PLL tracking system. These tracking loops are depicted in Figure 6. The input to the coupled loops is the time series of complex baseband-mixed samples for the given channel, as output in the lower-right corner of Figure 4. This input time history enters the combined tracking loops in the upper left-hand corner of Figure 6.
Block diagram of coupled DLL and PLL tracking loops for a single receiver channel
The outputs of the DLL and the PLL are, respectively, the time series of symbol start time estimates 
,… and the time series of (negative) beat carrier-phase estimates, 
,…. Each phase estimate applies to the corresponding symbol start time estimate. The DLL also outputs the slightly more accurate symbol start time estimates 
,…. These outputs are shown near the lower left-hand corner of Figure 6. The combined PLL/DLL discriminator calculations in the lower right-hand block of Figure 6 and the non-standard second-order DLL in the lower central block of the figure constitute this paper’s contributions to the area of OFDM signal tracking.
The DLL/PLL operations iterate once per symbol count i. For the i-th symbol, these calculations start with the DLL’s initial estimate of the midpoint time of this symbol, 
. The upper left-hand block finds the sample index lmid,i whose corresponding sample time falls nearest to this midpoint time:
9
Next, the system retrieves the 2,048 samples nearest this sample, i.e., the samples (lmid,i – 1024),(lmid,i – 1023),(lmid,i – 1022),…,(lmid,i +1023). These are the 2,048 samples that are output from the upper left-hand block of Figure 6. Next, the system pre-conditions these samples by multiplying them by the inverse of the h(t) windowing function and by mixing out the effects of the estimated carrier Doppler shift 
. The resulting pre-conditioned samples are:
10
The next calculation of the DLL/PLL is the 2,048-point FFT operation of the upper central block in Figure 6:
11
Each complex FFT output value 
corresponds to the nominal frequency offset from the carrier Δfk = kFs /2048. The frequency spacing between neighboring FFT points is Fs/2048 = 363.3728027343750 Hz.
The samples used in the FFT operations of Equation (11) have a nominal delay of 56 samples from the assumed initial time of the inverse FFT calculations that the transmitter uses to form the signal by employing the calculations of Equation (1). Therefore, it is necessary to compensate for this delay in order to get the resulting FFT outputs to separate into a distinct four-quadrant QPSK constellation in the complex plane. The mixing operation downstream of the FFT block in Figure 6 performs the needed compensation. Its mathematical form is:
12
The 56-sample delay in the data used in Equation (11) and the compensation applied in Equation (12) constitute this algorithm’s method of accounting for the digital OFDM signal’s cyclic prefix. Note that only the 382 frequencies that contain OFDM symbols are processed in this operation. The other 1,666 frequencies’ FFT outputs are discarded.
4.2 Symbol Decoding
The symbol decoding block in the upper right-hand corner of Figure 6 uses the delay-compensated FFT values Yik for k = −546,…, −356,356,…,546 in order to determine the symbol values nik for k = −546,…, −356,356,…546. Recall that the nik values can take on the BPSK values zero or two for the 22 reference frequencies k = −546,−527,−508,…, −356,356,375,394,…,546; and that they can take on the QPSK values zero, one, two, or three at the other 360 OFDM frequencies. Let these frequency indices be grouped into the following four index sets:
13
Thus, set 
contains the indices of the 11 BPSK reference frequencies in the lower OFDM band, set 
contains the indices of the 180 QPSK data frequencies in the lower OFDM band, set 
contains the indices of the 11 BPSK reference frequencies in the upper OFDM band, and set 
contains the indices of the 180 QPSK data frequencies in the upper OFDM band.
The symbol decoding process starts by computing the complex phases and magnitudes of the Yik symbol values:
14
The symbol decoding calculations first perform an ad-hoc approximate minimization of the following weighted phase fit cost function in order to develop estimates of the 191 symbols in the lower OFDM frequency band that fit a quadratic model of the frequency-dependent delay:
15
The unknown quadratic polynomial coefficients a0, a1, and a2 are allowed to take on real values. The 191 unknown quantities m(−546),…,m(−356) are restricted to take on integer values. Their optimized solution values will be used to compute the corresponding nik values. The magnitude weighting factors 
emphasize the need to fit the phases of the symbols with the largest complex magnitudes more than those of the symbols with the smallest complex magnitudes. The unknown constant a0 constitutes a group phase offset of all 191 complex values in the corresponding Yik data. The unknown coefficient a1 is a re-scaled estimate of a time advance of the true midpoint time of the received symbol relative to the sample time of the nominal midpoint tlmid,i,. The coefficient a2 allows for frequency variability from the average time advance. The coefficient factor (k + 451)/95 is a non-dimensional measure of OFDM frequency offset that ranges from −1 at the bottom of the lower OFDM band to +1 at the top of the lower band.
The cost function in Equation (15) is a mixed real/integer linear least-squares cost function. There exist exact methods to solve such problem (e.g., see Psiaki and Mohiuddin [2007]). Such techniques can be very expensive computationally. An ad-hoc minimization method is used here as a means of speeding the calculations. Although it is not guaranteed to find the exact global minimum, it often succeeds in finding the global solution.
The ad-hoc minimization of the cost function in Equation (15) proceeds as follows: Initially, only the first cost term summation is considered (i.e., the term that sums over the 11 frequencies 
). The first operation sets m(−546) = 0 and chooses m(−527),m(−508),m(−489),…,m(−356) so that each successive value of θik –πmk differs from the previous one by an amount with absolute value no more than π/2. This amounts to an unwrapping operation of the reference frequencies’ symbol phases by integer multiples of π. Next, these initial values of mk for 
are held fixed, and the three real-valued coefficients a0, a1, and a2 are optimized using standard linear least-squares techniques in order to minimize the first cost summation in Equation (15). Next, the integer unknowns are re-computed using the following formula:
16
Next, these new values of mk for 
are held fixed, and the three real-valued coefficients a0, a1, and a2 are re-optimized using linear least-squares techniques. The calculation continues iterating, with alternate evaluations of new integer mk estimates using Equation (16) followed by re-optimizations of the real-valued quantities a0, a1, and a2. Each re-optimization only considers the first cost summation term in Equation (15). The procedure terminates when all 11 of the new mk estimates from Equation (16) are unchanged from the previous iteration.
Next, the current estimates of a0, a1, and a2 are used to form estimates of the mk values for the lower OFDM band’s 180 data channels:
17
The approximate optimization next performs one more set of iterations. This set starts with the most recent estimates of the integers mk for all 
from Equations (16) and (17). It holds these values fixed, and it finds the real-valued quantities a0, a1, and a2 that optimize the entire cost function in Equation (15). It computes these optimal values by using linear least-squares techniques. Afterwards, the algorithm re-estimates the integers mk for all 
by using Equations (16) and (17). This process continues with an alternate determination of new real-valued a0, a1, and a2 by optimization of the cost function in Equation (15) followed by re-estimation of mk for 
by using Equations (16) and (17). This iteration continues until none of the integer-valued mk estimates change from their values in the previous iteration.
Next, the estimates mk for 
are used to compute the corresponding nik values as follows:
18
Afterwards, the value of ni(−470) is arbitrarily set to zero. The frequency index k = −470 corresponds to one of the 11 lower-band reference frequencies. As such, its BPSK symbol value will be ni(−470) = 0 or 2 before this operation. If it is already zero, then nothing is done. If it is two, then the following additional operation is carried out:
19
A similar sequence of calculations is used to determine estimates of nik for the upper OFDM band (i.e., for all 
). There are only two significant differences to these upper-band calculations. The first is that the frequency offset factor (k + 451)/ 95 in Equations (15)–(17) is replaced by the factor (k – 451)/95. The second difference is that the final step associated with Equation (19) is modified to arbitrarily ensure that ni470 = 0, which applies to one of the upper-band BPSK reference frequencies.
Finally, the symbol calculations give initial consideration to the possibility of a half-cycle offset between ni(−470) and ni470. An estimate of whether there is a half-cycle slip is formed by optimizing the following mixed real/integer linear least-squares cost function:
20
where 
is an estimate of the (negative) beat carrier phase at time 
is an estimate of the difference between the true symbol midpoint time and the time of the nominal midpoint sample tlmid,i; ΔmBA is an unknown integer that is used to allow an integer number of half-cycle slips between the lower and upper bands; and Δωk = 2πΔfk is the frequency offset of the k-th OFDM band given in radians/sec. This mixed real/integer linear least-squares problem is easily solved using the exact techniques of Psiaki and Mohiuddin (2007) because it has only a single integer-valued unknown. The only output of this last optimization that is retained for later consideration is the estimated delay 
.
No analysis has been made of the resulting bit error rates of these techniques. They were implemented in an ad-hoc manner without reference to whether better techniques might be available. In the future, it would be useful to measure the performance of these techniques relative to established techniques and, if they have poor performance, to replace them.
4.3 Optimal Estimation of DLL and PLL Discriminator Outputs
The DLL/PLL discriminator calculations in the lower right-hand block of Figure 6 perform nonlinear least-squares optimization of the following two cost functions:
21
and:
22
where the nik symbol values used here are those determined in the previous sub-section. Cost function J0 assumes that there is no half-cycle slip between the lower OFDM band and the upper band. Cost function J1 assumes that there is such a slip, which is why its second term has a positive sign in front of Ai.
The non-dimensional factors αk allow for the different frequency bands to have different nominal amplitudes. The standard deviations σk allow for the modeled standard deviations for the measurement errors in the real and imaginary parts of Yik to differ in different frequency bands. The possibility of having different amplitudes and different amounts of noise in different frequency bands allows for the presence of frequency-dependent channel effects, such as multipath.
This paper’s discriminator calculations determine its αk and σk values by considering the FFT component complex magnitudes, ρik for all 
or 
. The αk and σk values are computed by breaking the 382 OFDM frequency bands into 20 contiguous bands. They are the 20-component band from k = −546 to −527; the 19 component bands k = −526 to −508, k = −507 to −489, k = −488 to −470, …, k = −374 to −356, k = 356 to 374, k = 375 to 393, k = 394 to 412, …, and k = 508 to 526; and the additional 20-component band k = 527 to 546. For each of these 20 bands, a single pair (αk, σk) is calculated as follows. Suppose that γ is the mean value of 
for a given one of these bands and that η is the corresponding standard deviation of 
. That is, 
and 
, with mean and standard deviation being computed in the usual manner for the finite number of 
samples in the given band.
The values of αk and σk that apply to each 19- or 20-frequency band are then computed as follows:
23
where the number 20 changes to 19 in two places in the final equation if there are only 19 bands rather than 20. These calculations presume that the noise-induced variations in the real and imaginary parts of each Yik are all sampled from an identical zero-mean Gaussian random distribution for each frequency band and that each Yik in the band has the same complex amplitude. The choice between the maximum of β and γ / 4 in the second of this set of formulas is an ad-hoc method of ensuring that the nominal amplitude cannot be too small.
Under normal circumstances β would be the larger of the two values. The normalization in the final line makes all of the αk non-dimensional, and it ensures that the mean power of the αk values over the 20 bands is one. The units of the standard deviation σk are the same as the units of Yik, which are FFT RF front-end output units.
The optimal estimation cost functions in Equations (21) and (22) are non-linear in their three unknowns. A partial change of variables to the unknowns 
and 
makes the cost functions quadratic in the alternate unknowns 
and 
. Therefore, the optimal values of 
and 
can be computed exactly via linear algebra calculations for any given guess of the unknown delay 
. This modification allows the final nonlinear optimization calculations to be carried out in the single unknown 
.
A Newton’s-method optimization algorithm (Gill et al., 1981) has been used to minimize both of the final cost functions, J0 and J1 with respect to 
. Each cost function is evaluated at the corresponding optimal 
and 
values for each Newton’s-method iteration to improve the guess of 
. These final optimizations are carried out subject to minimum and maximum constraints in 
that take the form:
24
where 
is an a-priori estimate of 
, perhaps available from the DLL, and δτmid,i is a measure of the uncertainty in this a-priori estimate. The particular implementation of Newton’s method used here is restarted from multiple first guesses of 
that lie within this constrained region. Therefore, there is a high probability that the method will converge to the global minimum. One of the first guesses is the 
value that has been determined via optimization of the cost function in Equation (20) of the preceding subsection—provided that it respects the limits in Equation (24)
After convergence, the optimal estimates of Ai and 
are computed as follows:
25
After optimizing both J0 and J1 the resulting 
and 
estimates from the smaller of the two optimized cost functions are used as the final estimates. If J0 is the smaller of the two optimized cost functions, then the symbol values from the preceding subsection are considered valid as computed using Equations (16)–(19) for the lower OFDM band and their counterparts for the upper band. If J1 is the lower of the two optimized cost functions, however, then a half-cycle slip is deemed to have occurred between the lower and upper bands. In that case, the upper-band symbol estimates are modified as follows:
26
The DLL/PLL block diagram in Figure 6 includes the option to skip computing the nik symbols and to use externally supplied symbols instead. This option is indicated by the switch shown below the upper right-hand block. The use of nik symbol values that have been estimated in the upper right-hand block of Figure 6 makes the resulting discriminators decision-directed discriminators.
If pre-computed, externally-supplied symbol values are used, on the other hand, then the discriminators are not decision-directed. It may be wise to use externally supplied symbols if the signal is too weak to yield a sufficiently low probability of producing errors in the decoded BPSK reference symbols and QPSK data symbols. In such cases, the needed symbols might be provided by the reference station receiver of Figure 1. (Presumably its symbol estimates would have low error rates due to operating in a benign strong-signal environment.) In this case, only the J0 cost function in Equation (21) is optimized because the possibility of a half-cycle slip between the upper and lower bands is ruled out by the provision of reliable symbols. If possible, it would be best to avoid this need for external aiding because the communication channel from the reference station to the roving user receiver would have to transmit 255.6 K bits per second in order to supply all of the nik symbol information.
It may be possible to work with weaker signals without the need to obtain symbols from a reference station. Instead, one might employ the forward error correction capabilities of digital FM OFDM signals. This possibility has not been considered in the present paper.
The frequency-domain optimal data fitting problems in Equations (21) and (22) appear to compute the DLL discriminator output 
in a completely different manner than the traditional GNSS time-domain method of looking for a cross-correlation peak. In reality, the two methods yield the same results. One can show that the frequency-domain data fitting problem is equivalent to using the nik symbols in order to reconstruct the time-domain symbol envelope and then find the optimal alignment between the re-constructed envelope and the received time-domain signal that yields the highest cross-correlation peak. This time-domain version of the calculations is exactly what traditional GNSS DLL discriminators seek to implement.
Note that the DLL and PLL discriminator calculations developed here may be non-standard in OFDM signal processing. They make no distinction between reference subcarrier frequencies and data subcarrier frequencies. A typical conservative approach would use only the reference subcarriers for purposes of timing and phase estimation, as in Shamaei and Kassas (2018). The present approach implements, in effect, a set of decision-directed discriminators that rely on decoded data in order to develop a more precise discriminator output if the data decoding has been successful.
In both this subsection and the preceding subsection, no comparisons have been made with the existing state of the art for OFDM signal processing in commercial digital FM radios. The authors tried to find what that might be, but failed to find helpful references. Perhaps commercial receiver manufacturers use proprietary techniques.
4.4 PLL Kalman Filter
This subsection describes the Kalman filter that implements most of the PLL feedback algorithm which operates in the second-from-bottom block in the middle of Figure 6. It is structured as a linear time-varying Kalman filter. It is largely borrowed from the Kalman-filter-based PLL found in the work of Psiaki (2001). Its three-element state vector is:
27
where 
is the negative beat carrier phase in radians at DLL symbol start/ stop time 
is the PLL’s baseband-mixing version of the (negative) beat carrier phase; 
is the carrier Doppler shift in radians/sec at this same time; and 
is the carrier Doppler shift rate in radians/sec2 at this same time. Note that the PLL estimated negative beat carrier phase 
is generally somewhat less accurate than the estimate that would be provided by adding the first element of the Kalman filter’s xPLL,i estimate to 
.
The Kalman filter’s state dynamics propagation takes the form:
28
and the corresponding PLL (negative) beat carrier phase dynamic propagation model takes the form:
29
where 
. Recall that 
is the PLL’s rough estimate of the carrier Doppler shift, in radians/sec, for the symbol interval from 
to 
. It is generally less accurate than the average of the second elements of 
and 
. The state vector 
is the filter’s a-posteriori state estimate at time 
, and 
is its a-priori state estimate at time 
.
Note that there is potential for confusion in the use of the overstrike (-) notation. In this paper, it is used both to define PLL- and DLL-derived rough estimates, such as 
, and 
, and Kalman filter a-priori estimates, as in 
. Careful attention to the context in which this overstrike is used should avoid any confusion. The re-use of this overstrike for both types of quantities is somewhat justified by the fact that both types of estimates are not as good as the filter’s a-posteriori estimates. It is important to note, however, that quantities such as the second element of 
and 
are not identical, even though they are rough estimates of the carrier Doppler shift at the same time.
The PLL Kalman filter computes a measurement innovation for use in its measurement update. This innovation is calculated via the following operations:
30
The first line of these operations computes a raw innovation by adding the cumulative integer multiple of half-cycle slips ϕhc,i to the PLL discriminator value 
from the previous subsection, and it subtracts the Kalman filter’s a-priori modeled value of this measurement of the average (negative) beat carrier phase for the symbol interval. The next two lines compare this raw innovation with the final innovation of the previous symbol period, and they subtract whatever integer multiple of π radians is needed in order to make the final innovation νPLL,i differ from the value for the previous symbol by no more than π/2 radians. This operation takes out any sudden unphysical jumps of ±π radians that might be caused by BPSK bit flips on the k = −470 reference frequency. It also compensates for any 2π cycle ambiguities that can arise from the atan2(,) operation in Equation (25). The final line in Equation (30) updates the cumulative sum of the half-cycle slips that have been used to compensate the innovations.
The PLL Kalman filter finishes its operations with a measurement update:
31
where LPLL is the 3 × 1 Kalman filter gain matrix. It is a fixed quantity and is chosen using pole placement techniques in a manner that causes the nominal closed-loop error dynamics state transition matrix:
32
to have equivalent continuous-time eigenvalues that lie on a three-pole Butterworth pattern with a given bandwidth. Given the desired PLL Butterworth pattern bandwidth of BPLL Hz, the desired closed-loop eigenvalues of ΦPLLcl are e−2πBPLLTs, 
, and 
. Recall that the nominal symbol interval Ts is the nominal value of the i-th symbol duration 
.
One might argue that this Kalman filter is actually an observer because its gain matrix has been designed using pole placement rather than the steady-state Riccati equation. Consider, however, the experience of the first author with systems that have a scalar measurement and lack open-loop stability: It is often possible to choose the process noise and measurement noise covariance matrices that enter the steady-state Riccati equation in a way that yields exactly the same gain matrix as a pole placement calculation. Therefore, it is reasonable to call this a Kalman filter despite the pole-placement method of designing its gain matrix LPLL. The same can be said for the DLL Kalman filter that is developed in the next subsection.
The PLL Kalman filter has the option not to use feedback if the signal-to-noise ratio (SNR) is too low. A low SNR is indicated by a low 
amplitude estimate relative to the value of the estimated noise power in the optimized J0 or J1 cost function from the previous subsection. If the SNR is deemed to be too low, then the measurement update in Equation (31) is performed using LPLL = [0;0;0] in place of its usual value. In that case, the last two lines in Equation (30) are replaced by VPLL,i = VPLL,i–1 and ϕhc,i+1 = ϕhc,i.
The PLL changes slightly if it works with known symbols nik instead of using estimated symbols. In that case, there will not be any half-cycle slips due to bit changes on the k = −470 reference frequency. There will only be full-cycle ambiguities due to the use of the atan2(,) operation in Equation (25). In that situation, the second line of Equation (30) must be changed as follows: The value π must be replaced by the value 2π in the two places where it occurs in the equation.
4.5 DLL Kalman Filter
This subsection presents the DLL Kalman filter algorithm that implements most of the operations in the bottom block in the middle of Figure 6. The DLL is a non-standard algorithm that uses a second-order proportional/integral (PI) feed-back controller and carrier aiding. Typical GNSS DLLs only require a first-order proportional feedback controller because carrier aiding does a very good job of keeping track of high-frequency variations of the code start/stop times. The DLL feedback in a GNSS receiver only has to do two things: a) null out initial large uncertainties, and b) counteract the effects of the very slow code/carrier divergence that is caused by the ionosphere. As will be shown in a later section, the code/carrier divergence of a typical FM signal is much larger due to transmitter clock effects. This is the reason why a second-order PI DLL is needed.
The DLL’s two-element state vector is:
33
where τi is the OFDM symbol start/stop time, as already described above, and δτi is an increment to the nominal symbol interval Ts that is caused by code/carrier divergence.
The DLL Kalman filter’s carrier-aided dynamic propagation takes the form:
34
where 
is the filter’s a-posteriori estimate at the start of symbol i and 
is the filter’s a-priori estimate at the start of symbol i +1. The carrier-aided nominal time increment in the last term on the right-hand side of this equation is a standard calculation that uses the nominal carrier frequency fc, the nominal symbol period Ts, and the PLL Kalman filter’s estimate of the average carrier Doppler shift during the symbol interval 
.
The δτi state provides an additional means by which the time increment τi+1 – τi can differ from Ts beyond the difference caused by a non-zero carrier Doppler shift. In a later section of this paper, it will be shown why this capability is needed. This extra state constitutes the means by which the DLL Kalman filter implements the non-standard I part of its second-order PI feedback law.
The DLL Kalman filter also computes an innovation. It is:
35
where the notation ()1 indicates the first element of the vector in question. The raw innovation νDLLraw,i, equals the difference between the measured midpoint of the symbol interval, as determined using the DLL discriminator output 
from a previous subsection, and the a-priori estimate of the midpoint time. The final innovation clips the raw innovation in order to limit its absolute value to be no greater than the sample interval Δts.
The DLL Kalman filter finishes with its measurement update:
36
with LDLL being the 2 × 1 Kalman filter gain matrix. As with the PLL, it is a fixed quantity. It is designed using pole placement in order to cause the nominal closed-loop error dynamics state transition matrix:
37
to have equivalent continuous-time eigenvalues that lie on a two-pole Butterworth pattern with a given bandwidth. Given the desired DLL Butterworth pattern bandwidth of BDLL Hz, the desired closed-loop eigenvalues of ΦDLLcl are 
and 
.
Note that the DLL feedback can also be turned off if the SNR is too low. If this condition occurs, then the measurement update in Equation (36) is performed with, in effect, the feedback gain matrix set to LDLL = [0;0].
4.6 DLL and PLL Feedback Laws Based on their Kalman Filter State Estimates
The DLL Kalman filter’s state estimate is used to generate the 
DLL output value shown in Figure 6. This predicted symbol start/stop time is computed as follows:
38
The first term on the right-hand side of this equation gives the contributions of the filter’s current best estimate of τ+1 and its best estimate of δτi+1. The second term gives the PLL carrier-aided estimate of the interval from the (i+1)st symbol start/stop time to the (i+2)nd symbol start/stop time. Similarly, the third term on the right-hand side gives the PLL carrier-aided estimate of the interval from the (i+2)nd symbol start/stop time to the (i+3)rd symbol start/stop time.
The PLL Kalman filter’s state estimate is used to generate the 
PLL output value shown in Figure 6. This value is generated using the feedback law from Equation (16) of Psiaki (2001). It is repeated below using the notation of the present paper:
39
The feedback tuning parameter ζ must be in the range 0 ≤ ζ < 1. The value of ζ determines how fast 
will converge to zero. The value ζ = 0 yields convergence in two symbol periods if there is no noise in the system. A value of ζ close to one results in a convergence that is very slow.
These DLL and PLL feedback laws operate in a causal manner. They have been tested using after-the-fact signal processing in the present research effort, but they have been designed to be practically implementable in real time. Real-time implementability is the design criterion that led to the use of the delay blocks that appear in Figure 6.
4.7 DLL and PLL Initialization
The DLL and the PLL need their states to be initialized based on the acquisition results of the preceding section. The DLL state vector is initialized at:
40
where mopt is the maximizing integer for the test statistic in Equation (6). The estimate of the DLL’s second state is initialized at zero. There is no obvious way to ascertain this code/carrier divergence term a priori. It is typically near enough to zero for this initialization to yield good DLL convergence.
The PLL state vector is initialized at:
41
where ωDopp is the initial carrier Doppler shift estimate computed in Equation (8). The initial phase offset estimate in the first element of xPLL0 is set to zero because there is no easy way to determine a better initial estimate of this offset. Any arbitrary value seems to allow PLL convergence, and the value zero is chosen for convenience sake. The initial carrier Doppler shift rate estimate in the last element of xPLL0 is set to zero because there is no obvious way of ascertaining a better initial estimate. Typical values seem to be near enough to zero to enable good PLL convergence when starting from zero.
The PLL’s first two carrier Doppler shift outputs are initialized using the Doppler shift acquisition estimate from Equation (8): 
and 
. All subsequent PLL carrier Doppler shift outputs are determined by the PLL feedback law in Equation (39).
The DLL’s first three symbol start/stop time outputs are initialized using the mopt integer value that maximizes the acquisition test statistic in Equation (6) along with carrier aiding based on the acquisition’s estimate of the carrier Doppler shift: 
, and 
. All subsequent DLL symbol start/stop time outputs are determined by the DLL feedback law in Equation (38).
4.8 DLL and PLL Performance on Recorded Data
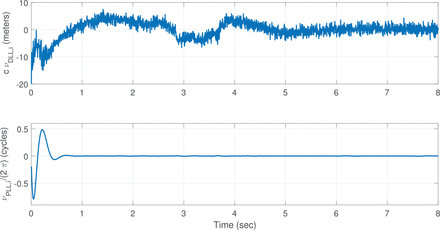
The coupled DLL/PLL tracking system of this section has been applied to numerous recorded sets of live FM data. Good performance has been obtained in all cases except some of those in which extreme multipath poses challenges. Figure 7 plots the convergence of the DLL innovations (top plot) and the PLL innovations (bottom plot) for a case that tracks the signal from the station at fc = 90.7 MHz in Charlotte, North Carolina. The second-order DLL’s Kalman filter for this case was tuned to a Butterworth pattern bandwidth of BDLL = 0.25 Hz. The third-order PLL’s Kalman filter was tuned to a Butterworth pattern bandwidth of BPLL = 2.50 Hz. The PLL feedback tuning parameter of Equation (39) was set to the value ζ = 0.9775.
Example Kalman filter innovations’ convergence for a DLL (top plot) and the corresponding PLL (bottom plot)
The plots in Figure 7 correspond to a static base station receiver. The corresponding plots for a roving receiver, which are not shown, are significantly noisier in steady-state for the DLL innovations, but not much noisier in steady-state for the PLL innovations.
These results show good convergence and good precision. The DLL reaches steady-state by about 6 seconds. Its innovations stay within about ±4 meters of zero after that. There is no apparent bias in the DLL innovations after 6 seconds. If a simple first-order DLL were used, then a significant bias would be present.
The PLL reaches steady-state much faster than the DLL by about 1 second. This faster convergence is expected because its bandwidth is 10 times larger than that of the DLL. The PLL’s innovations stay within about ±0.009 cycles (±3.3 deg) of zero after t = 1 sec. Thus, beat carrier phase can be tracked very precisely. This fact may indicate that accumulated delta range could be an accurate navigation observable of digital FM OFDM signals.
5 PSEUDORANGE AND ACCUMULATED DELTA-RANGE OBSERVABLES, SINGLE DIFFERENCES, AND THEIR PRECISION
5.1 Calculation of Pseudorange and Accumulated Delta Range
Pseudorange and accumulated delta-range observables can be computed in much the same way as they are computed for GNSS signals. If c is the speed of light in vacuum, then the pseudorange at the Kalman filter’s estimated symbol start/stop time 
is:
42
where 
is the start time of the i-th symbol according to the transmitter clock. As mentioned previously, symbols are grouped into contiguous sets of 32 that constitute frames. Each frame’s start is marked by the differentially encoded 7-bit synchronization pattern 0110010 on each of the 22 reference frequencies. Each reference frequency also differentially encodes a frame counter using another four of the frame’s 32 bits. These properties imply that each symbol’s start/stop time can be assigned a unique value based on its place relative to the frame synchronization pattern and based on the frame count. Therefore, one can define an absolute transmission time that is unique except for an ambiguity of 16 × 32 × Ts = 1.486077097505669 sec.
This ambiguity is easily resolvable between receivers within the listening area of a given station if the two receivers’ initial clock synchronizations are better than 1 second. This is true because a 1.486077097505669-second time ambiguity, if multiplied by the speed of light, translates into a distance ambiguity greater than the distance to the Moon.
The accumulated delta-range observable equals the change of the beat carrier phase since PLL tracking initialization translated into an equivalent distance:
43
The values ADRi and 
apply at estimated symbol start/stop time 
. The value of 
is computed as follows:
44
This formula corrects for the time difference between the best estimate of the symbol start/stop time, 
, and the rough DLL timing estimate at which the PLL state estimate in 
applies, which is 
.
5.2 Receiver-to-Receiver Single Differencing of Pseudorange and Accumulated Delta Range
The pseudorange and accumulated delta range defined in the the previous sub-section will have large errors due to transmitter clock drift. The clock stability requirements for FM broadcasting are very low, on the order of one part in 106. Therefore, single differencing between the roving user receiver and a reference receiver is needed in order to remove these clock drift errors. In order to successfully difference out transmitter clock drift, it is necessary to pair observables in the two receivers based on a common transmission time.
Suppose that the reference receiver is designated as Receiver A and that the roving receiver is designated as Receiver B. Suppose that the pseudorange, the accumulated delta range, the transmitter clock time, and the reception time at Receiver A are, respectively, PAl, ADRAl, 
, and 
for the l-th symbol start as counted by Receiver A. Similarly, suppose that the corresponding quantities for Receiver B are PBi, ADRBi, 
, and 
for the i-th symbol start as counted by Receiver B. Then the single-differencing calculations require that the proper symbol index l at Receiver A be found for a given symbol index i at Receiver B such that 
. Once the proper identification has been made between the two receivers, the required single-differenced pseudorange and accumulated delta range are calculated as follows:
45
These single differences apply at Receiver B clock time 
.
There exists the possibility of uncertainty about the correct association between 
and 
due to the 1.486077097505669-second transmitter timing ambiguity. An unresolved ambiguity can occur if there is a large synchronization uncertainty between the two receivers’ clock initializations. In this situation, a comparison can be made using one symbol’s 382 nik values for all 
. A comparison of these values between the two receivers should settle all questions about the correct resolution of the ambiguity.
If the nik values from the reference receiver are used by the roving receiver so that it does not estimate them itself, then all questions of transmission time synchronization must be settled at the time of signal acquisition. Synchronization can be accomplished by searching over a set of hypotheses about the proper pairing of known nik values with acquired symbol intervals. The search seeks a pairing that yields high correlation power (or, equivalently, low optimal estimation fit error) in the roving receiver.
5.3 Precision of Single-Differenced Observables
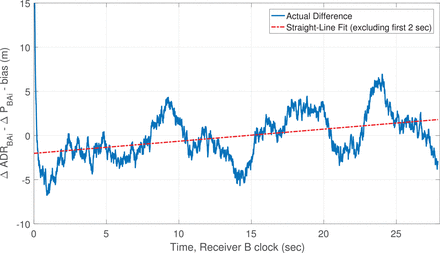
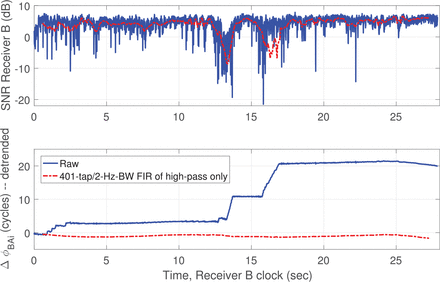
The obtainable precisions from single-differenced pseudorange and accumulated delta range have been analyzed by considering data from static receivers that were co-located in Roanoke, Virginia. Consider an example data set taken from Roanoke’s 89.1-MHz FM station. Figure 8 plots the time history of the difference between this signal’s single-differenced accumulated delta range and its single-differenced pseudorange. The plot was made after removing a large bias. The initial transient in the plot is the result of the DLL and PLL settling. After that, the plot should be flat. It appears to have a drift. A drift would constitute a code/carrier divergence.
Example of code/carrier divergence between single-differenced accumulated delta range and single-differenced pseudorange
This apparent code/carrier divergence cannot be caused by the ionosphere because the signal does not traverse the ionosphere. Thus, one must find a different explanation for this divergence than one might posit for a GNSS signal.
There is one main candidate for explaining this drift. It is a lack of phase-locked synchronization between the analog-to-digital converter (ADC) sample clock in the USRP RF-front end and its RF down-mixing signal’s synthesizer clock. Several analyses have been performed in order to assess whether the problem lies on the receiver end. An analysis of double-differenced accumulated delta range provided convincing evidence that the receiver does not have a clock phase synchronization problem.
Therefore, the apparent divergence of the single-differenced code and carrier remains a mystery. In looking closely at Figure 8, it seems possible that the apparent divergence is only a transient phenomenon caused by the shortness of the time span of the plot. A longer plot, had it been available, might have shown a flat curve on average.
Further insight into the precisions of these observables can be had by forming double differences. The resulting double differences are between two receivers and two radio stations—the 89.1-MHz and 92.3-MHz stations in Roanoke, Virginia. The two double-differences are defined as follows:
46
Note that the 89.1-MHz station’s symbol reception start/stop times did not exactly match those of the 92.3-MHz station. Therefore, interpolation of one station’s data to the other station’s start/stop times has been applied in order to compute the double differences. This interpolation is carried out using the common receiver clock time base of one of the two receivers.
Figure 9 plots these two double-differenced time histories. The upper plot shows the accumulated delta-range double-difference time history. The lower plot shows the pseudorange double-difference time history. The upper plot is encouraging. For static co-located receivers, one would expect the accumulated delta-range double-difference time history to reflect only the double-differenced carrier-phase bias. Therefore, one expects this plot to be constant. After initial PLL transients die out, the plot is constant to within about ±0.06 m. Therefore, accumulated delta-range single differences may provide navigation information to this level of precision. This fact gives rise to a hope that FM-based navigation might produce absolute accuracies on the order of 5 m or better for moving receivers if one uses carrier-phase-based navigation techniques and if there is sufficient receiver motion to render the single-differenced carrier-phase biases observable.
Example double-differenced accumulated delta-range time history (top plot) and double-differenced pseudorange time history (bottom plot) for co-located receivers and Roanoke stations 89.1 MHz and 92.3 MHz
Another important insight from the top plot of Figure 9 is the fact that it would display a noticeable slope if the code/carrier divergence problem were the result of a lack of phase-lock between the receiver’s ADC sample clock and its RF down-mixing synthesizer clock. There is no evident slope, which suggests a hypothesis that the code/carrier divergence of Figure 8 is caused by the transmitter.
The bottom plot of Figure 9 is troubling. The double-differenced pseudorange between two co-located receivers should be zero. After the settling of the initial DLL transients, the double difference in the bottom plot of Figure 9 settles to a range between +60 and +80 meters. This is very bad precision. It implies that digital FM OFDM pseudorange cannot provide navigation level accuracy, at least not for this case.
It is conjectured that the poor precision of the double-differenced pseudorange is caused by inter-frequency delay bias in the receivers’ electronics. Such a bias could be caused by differences between the receivers’ antenna and electronics phase versus frequency transfer function slopes at the two carrier frequencies. Such differences can occur in analog infinite-impulse-response filters.
There is a possibility that the observed pseudorange bias in the lower plot of Figure 9 could be calibrated and removed. This is a subject worthy of further study. Even if it were removed, however, the plot would still exhibit drifts on the order of ±10 m. This is a high level of imprecision for a navigation system that seeks to provide a backup or an alternative to current GNSS-based systems.
6 DATA WITH EXTREME MULTIPATH DISTORTION AND A MITIGATION STRATEGY
The precise result for an accumulated delta range in the top plot of Figure 9 inspired an attempt to do moving-vehicle navigation in Charlotte, North Carolina. The experiments were performed in Charlotte because the roving receiver needed to see at least four digital FM OFDM stations with a good geometric diversity if it wanted to do absolute 2D navigation using only single-differenced accumulated delta ranges. The required diversity was available in Charlotte, North Carolina, but not in the nearer city of Roanoke, Virginia.
The experiments involved a roving receiver that traveled along various freeways at speeds of about 65 mph. This speed was projected to give enough geometric variability of the line-of-sight vectors from the FM transmission towers to the roving receiver to enable sub-10-meter level absolute accuracy from accumulated delta range when using a data collection interval of 30 seconds.
A funny thing happened when the real data were collected and analyzed: High levels of time-varying multipath were observed at the roving receiver. This problem is clearly shown in Figure 10. The top plot shows the SNR of Receiver B computed for the individual FFT symbols and averaged over all of them. The bottom plot shows the corresponding single-differenced (negative) beat carrier phase between the roving receiver and the static reference receiver. This latter plot was made after applying a cubic detrending operation that caused the cycle slips to stand out clearly. Perhaps the magnitude of the challenge posed by multipath should have been less of a surprise given the significant body of work that has considered the problem of multipath when using terrestrial signals of opportunity, for example (Shamaei & Kassas, 2018; Wang & Morton, 2020).
Example of multipath effects in a rapidly moving receiver: rover signal-to-noise ratio (top plot) and cubically-detrended single-differenced beat carrier phase (bottom plot)
Note how the deepest fades in the solid blue curve on the top plot correspond to times of cycle-slipping in the solid blue curve on the bottom plot. In fact, these data look very similar to data for equatorial ionospheric scintillation (Humphreys et al., 2010). Although not shown in the figure, the data also exhibit the canonical fades noted in Humphreys et al. (2010) in which Receiver B’s tracked beat carrier phase exhibited rapid 1/2-cycle variations coincident with its deepest SNR fades.
Initial efforts to track Receiver B’s signals in this and similar cases led the authors to believe that their tracking algorithms or software were faulty. This concern led to the development of the tracking system that could work with pre-determined nik values and thereby provide a much better capability to track through deep power fades. The Receiver B results used to plot Figure 10 were generated using nik aiding from reference Receiver A. The latter receiver did not experience any deep power fades. After this change to a much more robust tracking method, the authors were able to examine the results more closely and realize that the anomalies were caused by extreme multipath interference rather than faulty tracking algorithms.
Despite the setback of this severe multipath, not all hope is lost. First, the slips in the single-differenced beat carrier-phase time history occurred only during the deepest fades of the Receiver B SNR. Furthermore, these slips occurred in integer numbers of cycles. Therefore, it may be possible to navigate using accumulated delta range if one omits data during deep power fades and if one estimates the beat carrier-phase integer-valued cycle slips that occur during the deep fades.
Another hopeful development is indicated by the dash-dotted red curves in Figure 10. These curves have been generated by attempting to repair the beat carrier phase tracking results in Receiver B through the exploitation of frequency diversity between the direct and multipath signals. The method works as follows: It starts by reconstructing a single pair of equivalent in-phase and quadrature accumulation measurements for each symbol interval. These accumulations are wide-band at the symbol frequency in the sense that they are not filtered by the PLL. They capture all of the net phase and amplitude variations that are caused by noise and by multipath.
Next, the method operates on successive overlapping batches of such samples, with each batch centered around a given symbol start time of interest. It performs a nonlinear optimization to find the carrier Doppler shift that provides the largest signal power after the Doppler shift is used to mix the (I,Q) samples to baseband and after the resulting baseband (I,Q) samples as passed through an FIR low-pass filter. In effect, these operations implement a band-pass FIR filter. The nonlinear optimization looks for the band center frequency that produces the highest power. The method then uses this optimum frequency and the corresponding band-pass-filtered (I,Q) accumulations in order to reconstruct the SNR and the beat carrier phase.
In another version of this technique, the optimization considers two terms. One is the band-pass filter’s output power. The other term is the nearness of the optimizing frequency to the optimized frequency from the previous batch of (I,Q) samples. This technique produced the dash-dotted red curves in Figure 10. Such a technique might enable more of the single-differenced beat carrier phase to be recovered and used for navigation despite strong multipath distortion.
Another benefit of this new signal processing method is its ability to scan for multiple power peaks in the frequency domain. This capability has been used to determine that multiple multipath signals occur sometimes and that one or more multipath signals are sometimes stronger than the direct signal. In hindsight, this latter fact seems obvious because of the deep fades in the top plot of Figure 10.
Channel estimation techniques such as ESPRIT (Roy & Kailath, 1989) and related methods offer another possible avenue for multipath compensation (Shamaei & Kassas, 2018; Wang & Morton, 2020). Such techniques should be considered for FM OFDM signals. It is beyond the scope of the present paper to explore such techniques.
7 INITIAL ATTEMPT TO DO PSEUDORANGE-BASED ABSOLUTE NAVIGATION
An attempt has been made to conduct single-differenced-pseudorange-only navigation using some of the Charlotte, North Carolina, data. The results for one of these attempts are shown in Figure 11. The filter that was used to produce these results was a sequential filter that estimated a new receiver position and a new single-differenced receiver clock offset at each sample, with samples spaced every second. The filter used rover/reference-station single-differenced pseudorange for the following Charlotte, North Carolina, FM stations: 89.9, 90.7, 95.1, 99.7, 103.7, 104.7, and 107.9 MHz. The filter also estimated six inter-frequency pseudorange biases for the stations 90.7, 95.1, 99.7, 103.7, 104.7, and 107.9 MHz measured relative to the station at 89.9 MHz. They were assumed to have a-priori values of zero with a-priori standard deviations of 350 m. This choice of estimated inter-frequency biases implies that the single-differenced receiver clock offset applies to time as defined by reception of the 89.9-MHz signal at the two receivers. No attempt has been made to delete samples where severe multipath may have degraded the pseudorange observables.
Results for single-differenced pseudorange navigation with inter-frequency bias estimation; the rover was traveling on Route 485 in Charlotte, North Carolina
The filter works by solving a batch-like problem that forms its estimates at sample time tk via minimization of the following cost function:
47
The estimated quantities are 
, the Earth-centered, Earth-fixed (ECEF) position vector of user Receiver B, cΔδBAk, the single-differenced range-equivalent clock offset between user Receiver B and base station Receiver A that applies to the 89.9-MHz band, and the 6 × 1 vector c∇ΔδBA, which contains the double-differenced range-equivalent clock offsets differenced between the two receivers and between the 89.9-MHz band and the other six bands.
The first two estimated quantities are assumed to vary between samples in a completely unmodeled manner. The vector of double-differenced range-equivalent clock offsets is presumed to remain constant because it is a property of the pair of receivers. The minimization of this cost function is carried out using a standard Gauss-Newton nonlinear least-squares algorithm.
Additional quantities in the cost function definition are: σpR, the single-differenced pseudorange measurement error standard deviation; 
, the single-differenced pseudorange for band l at sample time tk; 
the constant range from base station Receiver A to the antenna that transmits band l; 
, the known ECEF position vector of the antenna that transmits band l; al, the 6 × 1 vector that picks off the correct element of c∇ΔδBA for the l-th band; σalt, the pressure altimeter measurement error standard deviation; yaltk, the altimeter measurement at sample time tk; 
, the function that determines the WGS-84 altitude of the ECEF Cartisian position vector 
, the 6 × 1 vector that represents the optimal estimate of c∇ΔδBA based on all the solutions of similar estimation problems for sample times prior to tk; and 
, the 6 × 6 estimation error covariance matrix for the estimate 
. Note that the 6 × 1 vector a1 is all zeros for the l value that corresponds to the 89.9-MHz band. For the six other bands, it is a vector with zero in five of its rows and with one in the row that corresponds to the element of c∇ΔδBA which applies to band l.
The final cost term in Jnavk, the one involving 
and 
, is the only one that connects the estimation problems for different sample times. Thus, it is the only term that involves recursion. The optimal estimate of c∇ΔδBA for Jnavk becomes the vector 
when defining the next cost function Jnavk+1, and its corresponding computed covariance matrix becomes the matrix 
in the Jnavk+1. definition. The vector 
is initialized at zero, and the matrix 
is initialized at (350m)2 × I6×6 for the first sample.
The navigation results in Figure 11 show the system’s errors relative to ground truth as established by a GPS receiver that was also mounted on the rover vehicle. The rover vehicle was traveling along a freeway at high speed for this case. The results are not very good. Errors as large as 500 m occurred on the East axis—note the large negative bias on the solid red curve. There is obviously a problem with the altimeter calibration—note the 60-m vertical bias of the solid yellow/tan curve.
The authors have reason to believe that they will be able to improve markedly on these results when they incorporate multipath-compensated accumulated delta range, when they omit pseudoranges from times of severe multipath, and when they do a better job of calibrating the altimeter bias. This remains a work in progress.
8 ISSUES FOR FURTHER STUDY
There are a number of avenues for possible improvement to this system. The most promising of them are discussed briefly in this section.
The need to use outside aid to get the nik symbol data creates a high demand for transmission bandwidth from the reference receiver to the rover. Therefore, it would be good to develop methods to track signals during deep multipath fades without the need to resort to external symbol aiding. There are two possible avenues for maintaining lock during strong fades without the use of externally supplied symbols.
One avenue is to use only the 22 reference frequency bands for tracking and to try to predict their nik values. Their values may be easy to predict after tracking one or two frames of data. If so, then there would be no need of outside aid when using these predicted reference-band nik values to implement tracking. Another avenue for determining the nik symbol data in a standalone mode during deep fades is to use the digital FM OFDM signal’s forward error correction capabilities. Both of these ideas should be considered.
There exists a legacy digital FM signal that is present on almost all FM stations. It is called the Radio Broadcast Data System (RBDS) signal. The bits are sent at 19 KHz and are encoded on a 57-KHz sub-carrier that gets folded into the FM modulation of the analog voice/music signal. The authors have successfully used RBDS signals to compute single-differenced accumulated delta range for stations that do not have digital FM OFDM signals. An ability to use this alternate signal would improve the performance of an FM radio navigation system by increasing the number of available signals and, therefore, the geometric diversity of the radionavigation data. The main challenge to using RBDS signals is the potential difficulty of deciphering and tracking them during deep multipath-induced power fades.
A significant question concerns how well this system could navigate using the existing signals if one were to apply some of the best available signal processing techniques. The considered techniques should include excision of pseudoranges that are rendered unreliable due to high multipath. They should also include the use of multipath-corrected accumulated delta ranges and the estimation of integer-valued carrier-phase cycle slips during times of multipath-induced deep fades. Initial observability analyses have indicated that 5-m 2D positioning might be achievable if a sufficient geometric diversity of usable OFDM stations exists. More work needs to be done to test whether such accuracy can be realized in practice.
The strong multipath fades exhibited on the top plot of Figure 10 might be repeatable if they have been caused by terrain or buildings. If so, then the fades might themselves be usable for navigation purposes if they can be adequately mapped. This would constitute a special type of signal fingerprinting. At minimum, a follow-up experiment should be conducted over the same route in order to check whether the observed fades are repeatable.
Another interesting question concerns the usability of such techniques onboard aircraft. An advantage of an airborne system is that many more digital FM OFDM signals would be receivable at higher altitudes, thereby increasing the geometric diversity and enhancing the possibility that accumulated-delta-range-only absolute navigation could achieve sub-10-meter accuracy. The availability of more signals aloft is also a drawback of airborne operation.
It is likely that an aircraft would see multiple signals on the same frequency and that they would interfere with each other. This problem may be overcome by using aiding from nik data that were derived from ground-based reference stations in the vicinities of the corresponding FM transmitters. The nik data should be different for different stations that broadcast on the same frequencies. These data differences should enable the receiver to distinguish and track the two signals, just as differences of pseudorandom number codes enable a GNSS receiver to acquire and track multiple satellite signals that all broadcast on the same frequency. An airborne experiment should be conducted to test whether such techniques are practical.
Even if accumulated-delta-range-only techniques can be made to produce accurate solutions, one must keep in mind that such solutions require significant motion of the receiver. Another research topic might consider the question of how much initial motion would be needed to achieve a good fix and how long that fix could be maintained after motion had stopped.
One of the attractive features of FM navigation is the ability of the signal to penetrate buildings. Therefore, an important question concerns whether such techniques can be made to operate in an indoors environment.
9 SUMMARY AND CONCLUSION
This paper has developed and tested signal processing techniques for use in acquiring, tracking, and deriving navigation observables from digital FM OFDM signals. The goal of these developments has been to enable the use of FM signals as navigation signals of opportunity.
The techniques start with RF capture, baseband mixing, and digitization of the full FM band from 88 MHz to 108 MHz. Afterwards, digital signal processing techniques were used to extract the OFDM signals of individual stations. A given signal was then acquired using standard OFDM cyclic prefix correlation techniques. Next, the signal was tracked using a coupled DLL/PLL tracker that employed new decision-directed or externally-bit-aided discriminator calculations that were based on optimal estimation in the frequency domain. The DLL used a special second-order structure that was needed in order to compensate for the significant levels of code/carrier divergence that may have been caused by FM transmitters’ use of multiple non-phase-locked oscillators. The techniques developed here are applicable to many other OFDM signals of opportunity besides digital FM signals.
Pseudorange and accumulated delta-range navigation observables are computed using techniques that are like those used for GNSS signals. Afterwards, receiver-to-receiver single differences are computed in order to remove the effects of unknown transmitter clock offset and drift.
The new techniques have been tested using recorded versions of live digital FM data from Roanoke, Virginia, and Charlotte, North Carolina. Static tests were performed in Roanoke, and moving tests were performed in Charlotte. Static cases have demonstrated the potentially high precision of single-differenced accumulated delta ranges on the order of 0.06 m or better. Such results might enable absolute navigation using time series of accumulated delta ranges from four or more geometrically diverse stations if the roving receiver experiences sufficient motion over the filtering time interval.
Single-differenced pseudorange, however, exhibits inter-frequency timing biases as large as 100 m. It also exhibits much more time-varying drift than does the single-differenced accumulated delta range. These latter deficiencies are likely due to the relatively narrow bandwidth of the digital OFDM signals. The biggest challenge of the moving-receiver tests in Charlotte was the presence of extreme multipath interference. Efforts to compensate for multipath effects are ongoing.
A simple single-differenced-pseudorange-only navigation solution was attempted for one of the Charlotte data sets. The navigation filter included online estimation of the inter-frequency pseudorange biases starting with a-priori values of 0 ±350 m 1 –σ. The resulting navigation solutions were as much as 500 meters away from ground truth as provided by a co-mounted GPS receiver. Efforts are ongoing to improve upon these results through the incorporation of accumulated delta-range data and through compensation and/or excision of multipath-impacted data.
HOW TO CITE THIS ARTICLE
Psiaki, M. L., & Slosman, B. D. (2022) Tracking digital FM OFDM signals for the determination of navigation observables. NAVIGATION, 69(2). https://doi.org/10.33012/navi.521
This is an open access article under the terms of the Creative Commons Attribution License, which permits use, distribution and reproduction in any medium, provided the original work is properly cited.
Jump to section
- Article
- Abstract
- 1 INTRODUCTION
- 2 DIGITAL FM OFDM SIGNAL MODEL AND INITIAL PROCESSING
- 3 OFDM SIGNAL ACQUISITION
- 4 DLL AND PLL DISCRIMINATORS, TRACKING LOOPS, AND PERFORMANCE
- 5 PSEUDORANGE AND ACCUMULATED DELTA-RANGE OBSERVABLES, SINGLE DIFFERENCES, AND THEIR PRECISION
- 6 DATA WITH EXTREME MULTIPATH DISTORTION AND A MITIGATION STRATEGY
- 7 INITIAL ATTEMPT TO DO PSEUDORANGE-BASED ABSOLUTE NAVIGATION
- 8 ISSUES FOR FURTHER STUDY
- 9 SUMMARY AND CONCLUSION
- HOW TO CITE THIS ARTICLE
- REFERENCES
- Figures & Data
- Supplemental
- References
- Info & Metrics
Related Articles
Cited By...
- No citing articles found.